
张量分解-CP分解
CP分解(Canonical Polyadic Decomposition)
1927年Hitchcock提出了CP 分解。CP 分解将一个$N$阶的张量$\mathcal{X}\in {\mathbb{R}^{{I_1}{\mathbf{ \times }}{I_2}{\mathbf{ \times }} \cdots {\mathbf{ \times }}{I_N}}}$分解为$R$个秩为1的张量和的形式即:
\begin{equation}
\mathcal{X}=\sum \limits_{{r} = 1}^{{R}} \lambda_{r} a_{r}^{(1)}\circ a_{r}^{(2)}\circ \cdots a_{r}^{(N) }
\end{equation}
通常情况下$ a_{r}^{(n)}$是一个单位向量。定义$A^{(n)}=[a_{1}^{n} \quad a_{2}^{n} \quad \cdots \quad a_{R}^{n}]$,$D=diag(\lambda)$ 那么上面的公式可以写为:
\begin{equation}
\mathcal{X}=D\times_{1}A^{(1)}\times_{2}A^{(2)}\cdots\times_{N}A^{(N)}
\end{equation}
矩阵的表达形式即为:
\begin{equation}
X_{(n)}=A^{n}D(A^{(N)} \bigodot \cdots A^{(n+1)} \bigodot A^{(n-1)}\cdots
\bigodot A^{1})^T \label{eq:cpmatix}
\end{equation} 特殊的时候当张量$\mathcal{X}$的阶数为3的时候,它的分解的形式下图所示。
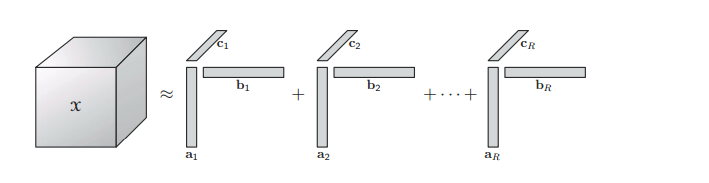
张量的低秩近似
在矩阵中定义最小的秩为1的矩阵和的个数为矩阵的秩,类似于矩阵的定义,$R$的最小值为张量的秩,记作$Rank(\mathcal{X})=R$,这样的CP分解也称为张量的秩分解。值得注意的是在张量中秩的定义是不唯一的,张量秩的个数求解是一个NP问题。对于一个矩阵$A$它的SVD分解定义为: \begin{equation} A =\sum \limits_{r = 1}^{{R}} \sigma_{r}u_{r} \circ v_{r},\quad \sigma_{1}\geq \sigma_{2}\geq \cdots \sigma_{R}\ge 0 \end{equation} 取SVD分解得到的前$k$个因子作为矩阵$A$的近似可以得到矩阵$A$的低秩近似。类似于矩阵中的定义我们取张量的前$k$个因子作为张量$\mathcal{X}$ 的低秩近似即: \begin{equation} \mathcal{X} =\sum \limits_{{k} = 1}^{{K}} \lambda_{k} a_{k}^{(1)}\circ a_{k}^{(2)}\circ \cdots a_{K}^{(N) } \label{eq:cp} \end{equation},不同于矩阵的低秩近似,张量的最佳Rank-n近似并不包括在其最佳Rank-n+1近似中,即张量的秩Rank-n 近似无法渐进地得到。
CP的求解
CP分解的求解首先要确定分解的秩1张量的个数,正如前面介绍的由于张量的秩Rank-n 近似无法渐进地得到。通常我们通过迭代的方法对$R$从1开始遍历直到找到一个合适的解。当数据无噪声时,重构误差为0所对应的解即为CP分解的解,当数据有噪声的情况下,可以通过CORCONDIA算法估计$R$。当分解的秩1张量的个数确定下来之后,可以通过交替最小二乘方法对CP分解进行进行求解。下面我们以三阶张量为例对ALS 算法进行阐述。
假设$\mathcal{X} \in \mathbb{R}^{I\times J \times K}$是一个三阶张量,对它进行张量分解的目标表达式为
\begin{equation}
\min \limits_{\mathcal{\hat{X}}} \| \mathcal{X}- \hat{\mathcal{X}\|},\quad
\hat{\mathcal{X}}=\sum \limits_{r=1}^{R}\lambda_{r} a_{r} \circ b_{r} \circ c_{r}=\left[\kern-0.15em\left[ {\lambda ; A,B,C}
\right]\kern-0.15em\right] \label{eq:cpobj}
\end{equation}
ALS算法首先固定$B$,$C$去求解$A$,接着固定$A$和$C$去求解$B$,然后固定$B$ 和$C$去求解$A$,这样不断地重复迭代直到达到收敛条件。固定矩阵$B$和$C$,可以得到上面的式子在mode-1矩阵展开的时候形式为
\begin{equation}
\min \limits_{\hat{A}}=\|X_{(1)}-\hat{A}(C \odot B)^{T} \|_{F}\label{eq:cpmode1}
\end{equation}
其中$\hat{A}=A.diag(\lambda)$,那么上述式子的最优解为
\begin{equation}
\hat{A}=X_{(1)}[(C \odot B)^{T}]^{\dagger}\label{eq:cpmode1solution}
\end{equation}
为了防止数值计算的病态问题,通常把$\hat{A}$的每一列单位化,即
$\lambda_{r}=|\hat{a_{r}}|,\quad a_{r}=\hat{a_{r}}/\lambda_{r}$
将上述式子推广到高阶形式可以得到
\begin{equation}
\begin{split}
&A^{(n)}=X^{n}(A^{(N)} \bigodot \cdots A^{(n+1)} \bigodot A^{(n-1)}\cdots
\bigodot A^{1} )V^{\dagger} \
&where \quad V=A^{(1)T}(A^{(1)} \bigodot \cdots A^{(n-1)} \bigodot A^{(n+1)}\cdots
\bigodot A^{(N)T}A^{(N)} )
\end{split}
\end{equation}
对于一个$N$阶的张量$X$它的ALS求解的步骤如下图所示。它假设分解出Rank-1 张量的个数$R$是事先知道的,对于各个因子的初始化,可以采用随机初始化也可以通过下面的式子进行初始化。
\begin{equation}
A^{(n)}=R \quad \text{ leading left singular vectors of} X_{(n)} \text{for} n=1,\cdots N
\end{equation}

可加约束
在一些应用中,为了使得CP分解更加的鲁棒和精确,可以在分解出的因子上加上一些先验知识即约束。比如说平滑约束(smooth)、正交约束、非负约束(nonegative) 、稀疏约束(sparsity)等。
CP分解应用
CP分解已经在信号处理,视频处理,语音处理,计算机视觉、机器学习等领域得到了广泛的应用 下面,以去噪为例,对CP分解在高光谱图像处理中的应用进行阐述。
高光谱图像(HSI)是上个世纪80年代以来新兴的一种新型成像技术,它包括了可见光和不可见光范围的几十到几百个连续光谱窄波段构成,形成了一种数据立方体结构的图像。高光谱图像可以看作是一个三阶张量,图像的空间域和光谱域构成了数据的三个维度。采用低秩CP分解对高光谱图像去噪认为低秩的部分是无噪声的部分,剩下的部分认为是噪声数据,它的示意图如下图所示。
 从图中可以看到一个高光谱图像数据$\mathcal{X}$ 可以由两部分组成即:
\begin{equation}
\mathcal{X}=\mathcal{S}+\mathcal{N}
\end{equation}
其中$\mathcal{S}$认为是低秩的部分即干净的图像,$\mathcal{N}$是噪声的部分(这里的噪声包括白噪声,高斯噪声等)。可以通过对原始数据$\mathcal{X}$ 进行低秩CP分解来得到$\mathcal{S}$。在Urban数据上进行去噪得到去噪前的数据和去噪之后的数据图分别如图下面的两幅图所示。从图中可以看到采用CP分解可以对高光谱图像进行去噪。
从图中可以看到一个高光谱图像数据$\mathcal{X}$ 可以由两部分组成即:
\begin{equation}
\mathcal{X}=\mathcal{S}+\mathcal{N}
\end{equation}
其中$\mathcal{S}$认为是低秩的部分即干净的图像,$\mathcal{N}$是噪声的部分(这里的噪声包括白噪声,高斯噪声等)。可以通过对原始数据$\mathcal{X}$ 进行低秩CP分解来得到$\mathcal{S}$。在Urban数据上进行去噪得到去噪前的数据和去噪之后的数据图分别如图下面的两幅图所示。从图中可以看到采用CP分解可以对高光谱图像进行去噪。

